Η κατακόρυφη δομή της ατμόσφαιρας μεταβάλλεται συνεχώς. Για την περιγραφή των μεταβολών αυτών χρησιμοποιούνται τρεις μετεωρολογικές παράμετροι: (α) η θερμοκρασία, (β) η πυκνότητα του ατμοσφαιρικού αέρα, και (γ) η ατμοσφαιρική πίεση.
Μεταβολή της θερμοκρασίας με το ύψος
Ο ρυθμός με τον οποίο η θερμοκρασία μεταβάλλεται με το ύψος μέσα στην ατμόσφαιρα ονομάζεται (κατακόρυφη) θερμοβαθμίδα. Η θερμοβαθμίδα ορίζεται ως η μεταβολή της θερμοκρασίας ανά μονάδα ύψους και εκφράζεται μέσα από την ακόλουθη σχέση:
Το αρνητικό πρόσημο χρησιμοποιείται για να δηλώσει την ελάττωση της θερμοκρασίας με το ύψος. Όπως προκύπτει από την παραπάνω σχέση, η μονάδα μέτρησης της θερμοβαθμίδας είναι οι oC/km ή oC/100 m.
Η τιμή της θερμοβαθμίδας μεταβάλλεται ανάλογα και με την ποσότητα της υγρασίας στην ατμόσφαιρα. Έτσι, η θερμοβαθμίδα διακρίνεται στην ξηρή αδιαβατική και την υγρή αδιαβατική θερμοβαθμίδα.
Η ξηρή αδιαβατική θερμοβαθμίδα είναι ίση με 1 oC/km. Σε αυτή την υποθετική περίπτωση θεωρούμε μία αέρια μάζα η οποία δεν περιέχει υδρατμούς και ανερχόμενη στην ατμόσφαιρα ψύχεται αδιαβατικά (δίχως ανταλλαγή θερμότητας με το περιβάλλον). Στην πραγματικότητα ωστόσο, κάθε αέρια μάζα περιέχει μικρότερη ή μεγαλύτερη ποσότητα υδρατμών. Για το λόγο αυτό, έχει επικρατήσει η χρησιμοποίηση μίας μέσης τιμής της θερμοβαθμίδας για τον υγρό αέρα της τροπόσφαιρας. Η θερμοβαθμίδα αυτή λαμβάνει τιμή ίση με 6-6.5 oC/km.
Η υγρή αδιαβατική θερμοβαθμίδα αναφέρεται στην περίπτωση μίας αέριας μάζας η οποία είναι κορεσμένη σε υδρατμούς και η οποία ψύχεται αδιαβατικά καθώς ανέρχεται στην ατμόσφαιρα. Είναι μικρότερη από την ξηρή αδιαβατική θερμοβαθμίδα εξαιτίας της συμπύκνωσης των υδρατμών η οποία απελευθερώνει θερμότητα, ελαττώνοντας με τον τρόπο αυτό το ρυθμό μεταβολής της θερμοκρασίας. Η μέση τιμή της υγρής αδιαβατικής θερμοβαθμίδας είναι ίση με 5 oC/km.
Υποθέτοντας ότι η θερμοβαθμίδα έχει μία σταθερή ή περίπου σταθερή τιμή, ολοκληρώνοντας τη σχέση ορισμού της παίρνουμε:
όπου Τ(z) και Τ(zo) είναι η θερμοκρασία σε ύψος z και zo, αντίστοιχα. Χρησιμοποιώντας την παραπάνω εξίσωση μπορούμε να υπολογίσουμε τη θερμοκρασία σε ύψος z όταν είναι γνωστή η θερμοκρασία σε ύψος zo και η θερμοβαθμίδα.
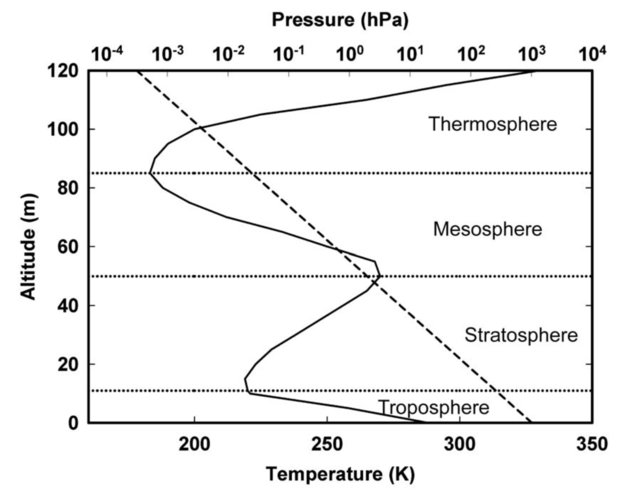
H καθ΄ ύψος μεταβολή της θερμοκρασίας με το ύψος μέσα στην ατμόσφαιρα απεικονίζεται στην Εικ. 1. Με βάση αυτή την κατακόρυφη μεταβολή της θερμοκρασίας ορίζεται και η φυσική στρωμάτωση της ατμόσφαιρας, όπως περιγράφηκε σε προηγούμενο άρθρο.
Μεταβολή της πυκνότητας με το ύψος
Η πυκνότητα του ατμοσφαιρικού αέρα (ρ) μπορεί να οριστεί ως η μάζα των ατόμων και των μορίων (m) ανά μονάδα όγκου (V):
Μονάδα μέτρησης της είναι το 1 kg/m3, ενώ χρησιμοποιείται συνηθέστερα το 1 g/m3.
Για τον προσδιορισμό της κατακόρυφης μεταβολής της πυκνότητας με το ύψος μέσα στην ατμόσφαιρα, χρησιμοποιείται η καταστατική εξίσωση των ιδανικών αερίων:
όπου p είναι η ατμοσφαιρική πίεση, R η παγκόσμια σταθερά των ιδανικών αερίων (ίση με 8.314 J/mol K), Μ το μέσο μοριακό βάρος του ατμοσφαιρικού αέρα και Τ η θερμοκρασία. Θεωρώντας ότι η ατμόσφαιρα βρίσκεται σε υδροστατική ισορροπία και ολοκληρώνοντας την παραπάνω σχέση για ένα ισόθερμο ατμοσφαιρικό στρώμα, καταλήγουμε:
όπου ρz η πυκνότητα σε ύψος z, ρο η πυκνότητα στην επιφάνεια, g η επιτάχυνση της βαρύτητας, Rα η ειδική σταθερά των αερίων (R/M) και Τ η θερμοκρασία.
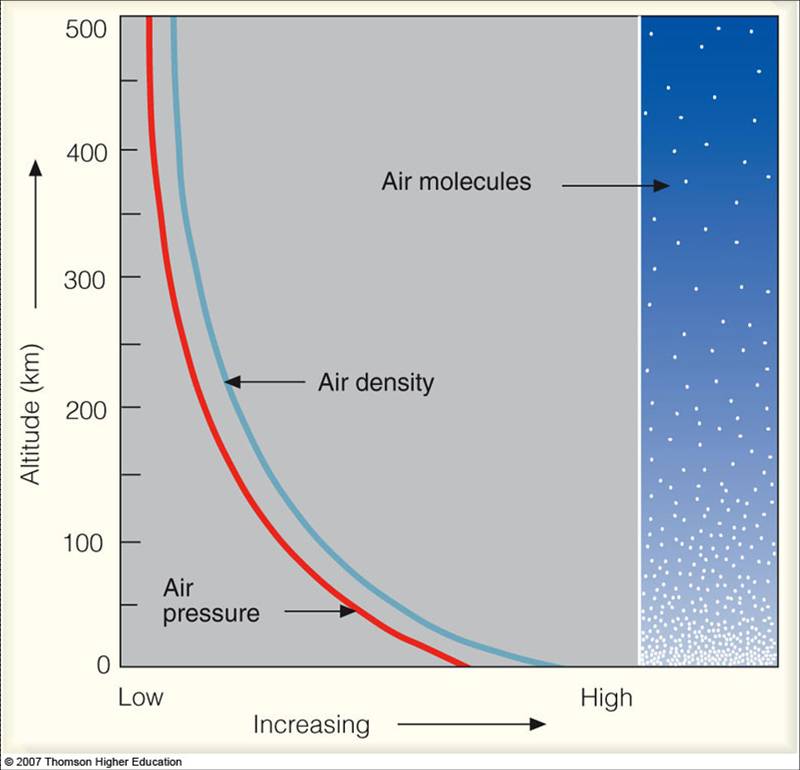
Με βάση την τελευταία σχέση, προκύπτει ότι η πυκνότητα ελαττώνεται εκθετικά με το ύψος μέσα στην ατμόσφαιρα, όπως φαίνεται και στο διάγραμμα της Εικ. 2. Με απλά λόγια, θα μπορούσαμε να πούμε ότι μέσα στην τροπόσφαιρα η πυκνότητα του ατμοσφαιρικού αέρα ελαττώνεται κατά ένα παράγοντα της τάξης του 10 για κάθε 17 km. Όσο πιο κοντά στην επιφάνεια βρισκόμαστε τόσο περισσότερο “πυκνός” είναι ο ατμοσφαιρικός αέρας. Αυτό είναι άλλωστε και το αναμενόμενο εάν αναλογιστούμε την επίδραση της δύναμης της βαρύτητας στα μόρια του ατμοσφαιρικού αέρα. Η επίδραση αυτή έχει ως αποτέλεσμα τη “συμπίεση” του ατμοσφαιρικού αέρα κοντά στην επιφάνεια της Γης, όπως φαίνεται και στο αριστερό τμήμα της Εικ. 2.
Μεταβολή της πίεσης με το ύψος
Η ατμοσφαιρική πίεση στην επιφάνεια της Γης ορίζεται ως η δύναμη (B) ανά μονάδα επιφανείας (Α) που ασκεί η υπερκείμενη της επιφάνειας στήλη του ατμοσφαιρικού αέρα. Με άλλα λόγια, η ατμοσφαιρική πίεση περιγράφει τη δύναμη (βάρος) που ασκεί μία ατμοσφαιρική στήλη στην επιφάνεια:
Μονάδα μέτρησης της πίεσης είναι το 1 N/m2. Στις ατμοσφαιρικές επιστήμες, ωστόσο, χρησιμοποιείται συνηθέστερα ως μονάδα μέτρησης το 1 mbar (1000 bar), όπου το 1 bar αντιστοιχεί σε δύναμη 10000 Ν ασκούμενη σε 1 m2 επιφανείας. Το 1 mbar είναι ταυτόσημη μονάδα με το 1 hPa, η οποία χρησιμοποιείται επίσης συχνά στη φυσική της ατμόσφαιρας.
Για τον προσδιορισμό της καθ’ ύψος μεταβολής της πίεσης χρησιμοποιείται η εξίσωση της υδροστατικής ισορροπίας. Με τον όρο υδροστατική ισορροπία περιγράφεται η κατάσταση εκείνη στην οποία η συνισταμένη των δυνάμεων που ασκούνται στην ατμόσφαιρα κατά τη κατακόρυφο διεύθυνση είναι ίση με μηδέν. Με άλλα λόγια, η υδροστατική ισορροπία “μεταφράζεται” σε απουσία κατακόρυφης επιτάχυνσης στην ατμόσφαιρα. Η θεώρηση αυτή δεν ισχύει σε καταιγιδοφόρα συστήματα, όπου και αναπτύσσονται ισχυρές κατακόρυφες επιταχύνσεις. Ωστόσο, η έκταση τέτοιων συστημάτων είναι μικρή συγκρινόμενη με την κατακόρυφη έκταση της ατμόσφαιρας, ώστε θεωρούμε ότι η τελευταία βρίσκεται πραγματικά σε υδροστατική ισορροπία.
Η εξίσωση που περιγράφει την υδροστατική ισορροπία (υδροστατική εξίσωση) είναι η ακόλουθη:
όπου το αριστερό μέλος αντιπροσωπεύει τη λεγόμενη δύναμη της βαροβαθμίδας (δύναμη που αναπτύσσεται εξαιτίας της μεταβολής της ατμοσφαιρική πίεσης) και το δεξί μέλος τη δύναμη της βαρύτητας. Η παραπάνω εξίσωση μας πληροφορεί πως ο ρυθμός μεταβολής της πίεσης με το ύψος είναι ανάλογος του γινομένου της πυκνότητας του αέρα επί την επιτάχυνση της βαρύτητας. Το αρνητικό πρόσημο υποδηλώνει την ελάττωση της ατμοσφαιρική πίεσης με το ύψος. Ολοκληρώνοντας την τελευταία εξίσωση για ένα ατμοσφαιρικό στρώμα με σχεδόν σταθερή θερμοκρασία (ισόθερμο) και λαμβάνοντας υπόψη την εξάρτηση της πυκνότητας από το ύψος (βλ. παραπάνω) καταλήγουμε:
όπου p(z) είναι η πίεση σε ύψος z, p(zo) η πίεση στην επιφάνεια, g η επιτάχυνση της βαρύτητας, R η παγκόσμια σταθερά των ιδανικών αερίων και Τ η μέση θερμοκρασία του ατμοσφαιρικού στρώματος. Η τελευταία εξίσωση είναι γνωστή ως υψομετρική εξίσωση. Όπως προκύπτει από αυτή, η ατμοσφαιρική πίεση, όπως και η πυκνότητα, ελαττώνεται εκθετικά με το ύψος μέσα στην ατμόσφαιρα. Το συμπέρασμα αυτό επιβεβαιώνεται και από την εξέταση του διαγράμματος της Εικ. 2. Ειδικότερα για την τροπόσφαιρα, η ατμοσφαιρική πίεση ελαττώνεται κατά ένα παράγοντα του 10 για κάθε 17 km.
Επιμέλεια-Σύνταξη: Θοδωρής Μ. Γιάνναρος, Φυσικός – Δρ. Φυσικής Περιβάλλοντος


